Problemas Clásicos
Aristarco
Aristarco de Samos, nació hacia el 310 a. C.
Puede considerarse como el mayor astrónomo de la antigüedad.
A él se deben las primeras estimaciones para calcular la proporción
entre la distancia de la Tierra al Sol y de la Tierra a la la Luna. Además,
Aristarco propuso un modelo astronómico heliocéntrico y heliostático,
adelantándose en 1.800 años al modelo de Copérnico.
Actividades
Distancias Tierra-Sol y Tierra-Luna
Las fases de la Luna vienen determinadas por las posiciones
relativas del Sol, la Tierra y la Luna. El Sol siempre ilumina media esfera
lunar, pero desde la Tierra unas veces vemos la semiesfera completamente
iluminada (luna llena) y otras sólo vemos una parte de la
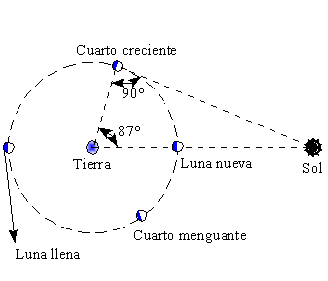
semiesfera (cuarto creciente o menguante) o no la vemos (luna nueva). Aristarco
dedujo que cuando la Luna estaba exactamente en cuarto creciente el triángulo
formado por la Tierra, la Luna y el Sol era rectángulo, ya que el
ángulo TLS era recto. Mediante la observación directa
podemos determinar el ángulo LTS, cuyo vértice es nuestro
planeta. Aristarco halló para este ángulo un valor
de 87°.
-
Calcula las razones entre las distancias Tierra-Luna y Tierra-Sol.
-
Aristarco se equivocó, por falta de medios técnicos, en la
medición del ángulo LTS. El valor real es de 89° 51´.
Repite el problema con esta nueva medida. Compara los resultados de este
apartado y el anterior.
-
Sabiendo que la distancia TS es de 150.000.000 Km aproximadamente, calcula
TL a partir de las relaciones obtenidas en los apartados a) y b).
Tamaños del Sol y de la Luna.
Al observar los eclipses de luna Aristarco pudo comprobar
que el cono de sombra proyectado por la Tierra, cuando lo atraviesa la
Luna, es de unas dos veces el tamaño del diámetro lunar.
Si llamamos RS, RT y RL a los radios
del Sol, la Tierra y la Luna respectivamente, y DS y DL
a las distancias Tierra-Sol y Tierra-Luna:
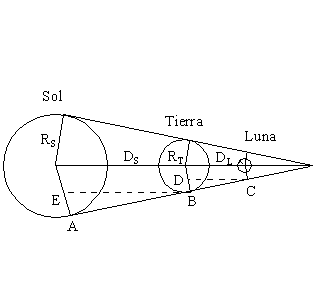 Demuestra por la semejanza de los triángulos
BCD y ABE que
Demuestra por la semejanza de los triángulos
BCD y ABE que 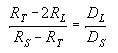 .
A partir de la relación anterior, tomando como DS=19DL
y RS=19RL, halla la relación que Aristarco
encontró para los radios del la Luna y de la Tierra.
.
A partir de la relación anterior, tomando como DS=19DL
y RS=19RL, halla la relación que Aristarco
encontró para los radios del la Luna y de la Tierra.
Eratóstenes (275-194 a. C.)
Uno de sus resultados más importantes es que
determinó con un error más que aceptable el radio de la Tierra
(por tanto, ya sabían que era redonda). Eratóstenes hizo
un mapa del mundo conocido. Considerando la limitación de los medios
de transporte de la época, su mapa del área mediterránea
es muy apreciable. Las zonas extremas del mapa son las más descuidadas,
por carencia de datos.
Actividades
Tamaño de la Tierra
Localiza Adra (Almería) y Sestao (Vizcaya) en
un mapa de España, calcula la distancia a que se encuentran; supongamos
que están situadas en un mismo meridiano. Calcula la latitud en
que se encuentran ambas ciudades.
-
Realiza un dibujo que represente los datos del problema.
-
¿Cuánto vale el ángulo formado por las semirrectas
que parten del centro de la Tierra y pasan por las dos ciudades?
-
Calcula el radio de la Tierra, y la longitud de un meridiano.
Cálculo del tamaño de la Tierra según Eratóstenes.
Eratóstenes conocía el hecho de que en
Siene (actual Assuan, ciudad de Egipto situada aguas arriba en el Nilo),
había un pozo muy profundo en el que el 21 de Junio, al mediodía,
los rayos solares incidían en el fondo. Admitió también
que ese mismo día y a la misma hora, en la ciudad de Alejandría
(situdad según él en el mismo meridiano más al Norte),
el Sol formaba con la vertical un ángulo de 1/50 del ángulo
completo. Puesto que el Sol está tan lejos de la Tierra, los rayos
solares deben llegar paralelos tal cual se ilustra en la figura, donde
A es Alejandría y S Siene:
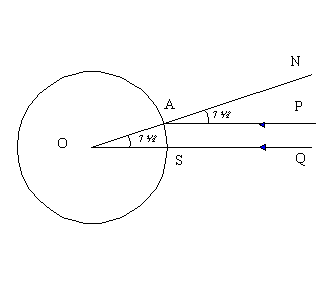
Sabía que Siene se encuentra a unos 5.000 estadios (unidad de
medida usada por los griegos) al Sur de Alejandría. Con estos datos
halla:
-
¿Cuánto vale el ángulo central?
-
¿Cuánto mide el radio de la Tierra en estadios?
-
Si admitimos que cada estadio es aproximadamente 157,5 metros, ¿cuál
es el valor que obtuvo Eratóstenes para el radio de la Tierra?
-
Con las dos ciudades anteriores (Adra y Sestao), ¿se puede resolver
el problema de forma análoga a como lo hizo Eratóstenes?
La mayor dificultad con que se encontró Eratóstenes
fue la de obtener una medida correcta de la distancia de Alejandría
a Siene; de hecho, Siene no está exactamente al Sur de Alejandría,
ni el Sol está precisamente encima de la ciudad ese día.
Hubo pues, en sus cálculos, tres fuentes de error, y Eratóstenes
tuvo la suerte de que el efecto de uno de los errores quedara casi compensado
por los de los otros dos, obteniendo un resultado más que aceptable.
-
Antes de Eratóstenes se realizó un cálculo de la circunferencia
de la Tierra usando la misma técnica. La única diferencia
fue que el ángulo fue medido en Lysimachia en vez de en Alejandría
los datos obtenidos fueron:
-
Ángulo de 1/15 del círculo completo.
-
Distancia entre esta ciudad y Siene = 20.000 estadios.
Con estos datos halla el radio de la Tierra en estadios y en kilómetros.
¿Qué resultado es mejor?
Jugando con el Calendario Juliano
Eratóstenes es el autor del calendario
Juliano, en el que cada 4 años hay uno que tiene un día
más. Esto supone admitir que el año tiene exactamente 365
días y ¼. Fue adoptado por los romanos bajo el gobierno de
Julio César, en el año 45 a. C. Como el año real contiene
algo menos de 365 días y ¼, este calendario produce un error
de unos 3 días cada 400 años. Para subsanar este error,
en 1582 el Papa Gregorio XIII establece un nuevo calendario (calendario
Gregoriano) en el que no son bisiestos los años cuyos números
sean divisibles por 100 pero no por 400 y, además, se suprimen diez
días (del 4-10-1582 al 15-10-1582). Así por ejemplo, 1800
y 1900 no han sido bisiestos; lo serán en cambio 2000 y 2400. El
error se reduce así a 1 día cada 4000 años aproximadamente.
-
Halla el número de años bisiestos que según el calendario
Juliano habría entre los años 2.000 y 3.000.
-
Haz lo mismo para el Calendario Gregoriano. Compara los resultados.
En 1582 José Scaliger fijó una escala
continua de tiempo fijando su origen el 1 de Enero del año 4713
aC a las 12 del mediodía, esta forma de contar el tiempo se llama
fecha
juliana. El applet que sigue calcula dicha fecha si le damos como
entrada una fecha en formato "actual". Por defecto toma como fecha de entrada
la fecha del ordenador. Para obtener la fecha juliana del 10 de Julio de
1997 a las 12 horas escribiremos Jul 10 12:0:0 1997 y debería obtenerse
2.450.640 como resultado. Hay que aclarar que el mes hay que escribirlo
con las tres primeras letras en Inglés, por ejemplo, enero se escribiría
Jan:
Usando este applet obtén:
-
La fecha juliana actual.
-
La fecha juliana del año 1 de nuestra era a las 12 del mediodia.
-
La fecha juliana del 4-10-1582
-
La fecha juliana del 15-10-1582. Comenta qué ocurre.
Claudio Ptolomeo
Claudio Ptolomeo, vivió durante el siglo II de
nuestra era. Su contribución no consiste en la aportación
de grandes ideas nuevas, sino en estudiar la gran cantidad de datos existentes
sobre el movimiento de los planetas y hacer un tratado que resumía
toda la Astronomía griega.
Al comienzo de su tratado Sintaxis Matemática
más conocido por el nombre árabe del
Almagesto, enuncia
los supuestos iniciales de su Astronomía:
-
"... los cielos son esféricos y se mueven circularmente a un eje
fijo"
-
"La figura de la Tierra es claramente esférica"
-
"La Tierra está exactamente en el centro de los cielos como un punto
geométrico"
-
"El objetivo que el astrónomo debe afanarse por conseguir es éste:
demostrar que todos los fenómenos del firmamento son producidos
por movimientos circulares y uniformes". "Cualquier figura distinta de
la circular que se suponga para el movimiento celeste, entrañaría
distancias desiguales desde la Tierra hasta las diferentes partes de los
cielos, lo que no se observa". "Además, nos hemos propuesto la tarea
de demostrar que las aparentes irregularidades de los 5 planetas, el Sol
y la Luna pueden representarse por medio de movimientos circulares y uniformes
porque sólo tales movimientos son apropiados para su divina naturaleza.
Y estamos autorizados a considerar el cumplimiento de esta tarea como el
objetivo último de la ciencia matemática basada en la filosofía".
-
"Todos los cuerpos pesados caen al centro de los cielos. Así pues,
la Tierra que es el más pesado de los 4 elementos (agua, aire, tierra,
fuego) cae al centro".
Explicación del sistema Ptolemaico.
Hay que distinguir entre planetas exteriores -Marte, Júpiter
y Saturno- y planetas interiores -Mercurio y Venus-.
-
Comencemos por los planetas exteriores y tomemos como ejemplo a Júpiter.
Júpiter necesita unos doce años para completar su traslación
aparente alrededor de la Tierra. No se mueve, además, a una velocidad
uniforme. Se mueve hacia el Este durante cierto tiempo; luego, durante
un tiempo más breve hacia el Oeste; luego otra vez hacia el Este,
y así sucesivamente. Los instantes en que no se mueve se llaman
estaciones.
Y el movimiento hacia el Oeste se llama retrógrado,
o recesiones. Se tiene que, además de durar menos,
el movimiento de recesión es más lento que el de progresión
hacia el Este. Por tanto, al final, el planeta se dirige hacia el Este.
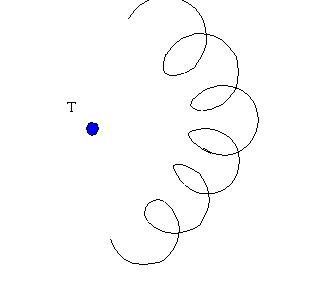
Consideremos la figura que sigue en la que T es la Tierra,
S el Sol y J júpiter:
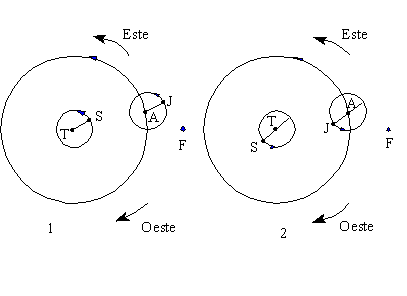
Supongamos que estamos mirando el dibujo
desde un punto situado en la vertical del Polo Norte de la Tierra y que
F es una estrella fija. El Sol gira alrededor de la Tierra, de Oeste a
Este, una vez en un año. El punto A se mueve alrededor de la Tierra,
también de Oeste a Este, con una traslación completa en unos
12 años. El círculo por el que se mueve A se llama deferente
de Júpiter. Júpiter gira mientras tanto alrededor de
A en un círculo menor llamado epiciclo, de forma que
AJ es siempre paralela a TS. Cuando la situación es la de la figura
1, el movimiento de J respecto de A tiene el mismo sentido que el de A
respecto de F. Visto desde T, J parece moverse de Oeste a Este a más
velocidad que A. Seis meses después, la posición será
la de la figura 2. El Sol ha recorrido la mitad de su órbita alrededor
de la Tierra, mientras que el punto A no ha recorrido más que 1/24
de la suya. AJ se ha movido manteniéndose paralela a ST, y el movimiento
de J respecto de A es ahora retrógrado. El movimiento de J en su
epiciclo es más rápido que el de A por el deferente. Por
tanto, visto desde T, J se mueve ahora de Este a Oeste pero no tan rápidamente
como se movía antes de Oeste a Este.
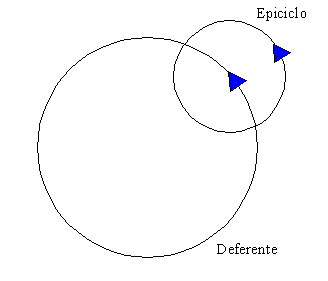
Con este modelo no se consiguió explicar
el movimiento aparente de Júpiter alrededor de la Tierra. En realidad,
Júpiter, no sigue exactamente el punto J (Figura 1). Para
explicar exactamente su movimiento aparente fue necesario introducir otro
punto J´ que describiera un epiciclo aún menor alrededor de
J, y aún un tercer punto J´´ que describiera un nuevo
epiciclo menor entorno de J´, y así sucesivamente. Júpiter
era el punto que describía el último de los epiciclos. Con
un cálculo meticuloso de las dimensiones y las velocidades de todos
esos epiciclos, y admitiendo que la Tierra no estaba en el centro del deferentePtolomeo
consiguió finalmente reproducir el movimiento aparente de Júpiter.
-
Para Mercurio y Venus la explicación que daba era diferente:
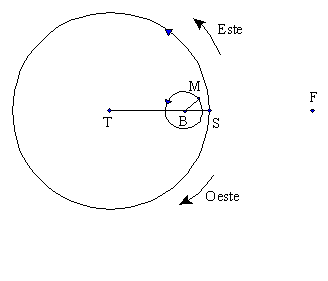 B es un punto situado en TS y, por tanto, gira con el
Sol alrededor de la Tierra una vez por año. Mercurio (M) describe
un epiciclo con centro en B y a la velocidad necesaria para cruzar TB cada
116 días aproximadamente. Visto desde T, Mercurio parece seguir
al Sol a través del Zodíaco, oscilando a uno y otro lado
del Sol.
B es un punto situado en TS y, por tanto, gira con el
Sol alrededor de la Tierra una vez por año. Mercurio (M) describe
un epiciclo con centro en B y a la velocidad necesaria para cruzar TB cada
116 días aproximadamente. Visto desde T, Mercurio parece seguir
al Sol a través del Zodíaco, oscilando a uno y otro lado
del Sol.
Actividades
 A
la combinación de movimientos consistente en que cada vez que el
planeta da una vuelta sobre el epiciclo mientras que el centro del epiciclo
da una vuelta sobre el deferente, ambos en el mismo sentido, la representaremos
con la notación (1e, 1d).
A
la combinación de movimientos consistente en que cada vez que el
planeta da una vuelta sobre el epiciclo mientras que el centro del epiciclo
da una vuelta sobre el deferente, ambos en el mismo sentido, la representaremos
con la notación (1e, 1d).
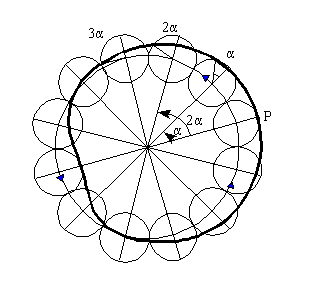
Como se puede ver en el dibujo, para obtener las posiciones sucesivas
del planeta y trazar aproximadamente su órbita, hay que medir los
ángulos como está indicado:
en la posición P´ el centro del epiciclo ha avanzado un
ángulo , arrastrando con él el propio epiciclo y al planeta
situado en él. A su vez, el epiciclo ha girado un ángulo
alrededor de su centro, de forma que la posición del planeta es
la indicad. En las posiciones sucesivas se miden los ángulos de
la misma manera.
-
Si con (Xe, Yd) notamos el epiciclo en el cual el planeta da X vueltas
sobre el epiciclo, mientras que el centro del epiciclo da Y vueltas sobre
el deferente (ambos en el mismo sentido), representa los epiciclos (3e,1d),
(5e,1d) y (5e,2d).



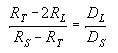 .
A partir de la relación anterior, tomando como DS=19DL
y RS=19RL, halla la relación que Aristarco
encontró para los radios del la Luna y de la Tierra.
.
A partir de la relación anterior, tomando como DS=19DL
y RS=19RL, halla la relación que Aristarco
encontró para los radios del la Luna y de la Tierra.




 A
la combinación de movimientos consistente en que cada vez que el
planeta da una vuelta sobre el epiciclo mientras que el centro del epiciclo
da una vuelta sobre el deferente, ambos en el mismo sentido, la representaremos
con la notación (1e, 1d).
A
la combinación de movimientos consistente en que cada vez que el
planeta da una vuelta sobre el epiciclo mientras que el centro del epiciclo
da una vuelta sobre el deferente, ambos en el mismo sentido, la representaremos
con la notación (1e, 1d).