Una recta paralela a un plano y perpendicular a otra en el espacio

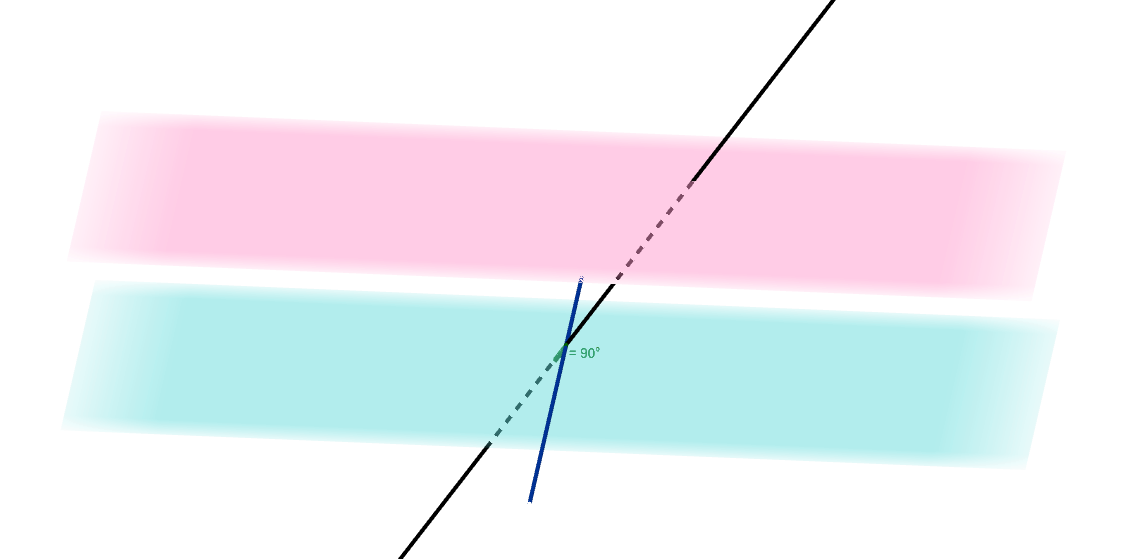
Vemos cómo determinar alguna recta del espacio con la condición de ser paralela a un plano y cortar perpendicularmente a otra. El fichero LyX/pythontex permite resolver este tipo de ejercicios para distintos valores de entrada. Los datos para resolver los problemas se pueden introducir de forma manual o de forma aleatoria. Se usa el módulo Geometry de sympy.

Lo único que tendremos que adecuar en el fichero es:

# Podemos trabajar con dos opciones:
# m --> Datos manuales.
# a --> Datos aleatorios a partir de puntos (con coordenadas enteras) del espacio.
# Si no ponemos que opción es "m" siempre se hace con datos aleatorios.
opcion = ''

# VALORES PARA LOS DATOS MANUALES
# Plano Pi, a partir de su vector normal y un punto
np = Point3D(1,0,1)
Pp = Point3D(1,0,1)

# Recta s definida por dos puntos
P1s = Point3D(-1,1,1)
P2s = Point3D(0,0,2)

# VALORES PARA LOS DATOS ALEATORIOS
# Valores mínimos y máximos para las coordenadas aleatorias enteras de los puntos.
vm = -5
vM = 5

tal cuál está por defecto, obtenemos un ejercicio con datos aleatorios. Un ejemplo de ejercicio obtenido de esa forma se muestra a continuación:

Ejercicio

Calcular alguna recta que sea paralela al plano de ecuación $\pi\equiv33x-9y-12z-87=0$ y corte perpendicularmente a la recta $s\equiv\begin{cases} y-5$ .

Solución

Se puede resolver de varias formas. Optaré por una que se basa en tener en cuenta que nuestra recta $r$ :

Está contenida en el plano paralelo al plano $\pi$ de ecuación $\pi_{0}\equiv33x-9y-12z=0$ , es decir, está contenida en el plano paralelo a $\pi$ que pasa por el origen de coordenadas. De esa forma me garantizo que $r\ || \pi$

$r\in\pi_{0}\Rightarrow$ el vector normal al plano $\pi_{0}$ ( $\vec{n}_{\pi}$ ) que es el mismo que el vector normal al plano $\pi$ (por ser paralelos) es perpendicular al vector director de la recta $r$ ( $\vec{u}_{r}$ )

Como $r\perp s\,\Rightarrow\vec{u}_{r}\perp\vec{u}_{s}$

De las dos cuestiones anteriores podemos deducir que $\vec{u}_{r}=\vec{u}_{s}\times\vec{n}_{\pi}$

Sea $P$ el punto de intersección de las rectas $r$ y $s\,\Rightarrow$ $\begin{cases} P$ es el punto de corte de la recta $s$ y el plano $\pi_{0}$ , es decir, es la solución del sistema determinado por las ecuaciones del plano y la recta anteriores .

A partir de lo anterior, calculemos [1]:

Normal al plano $\pi$ es $\vec{n}_{\pi}\equiv\left(33,\ -9,\ -12\right)\equiv\left(11,\ -3,\ -4\right)$

Director de la recta $s$ , lo podemos obtener de varias formas, por ejemplo:

Introduciendo parámetros en la ecuación de la recta $s$ y, si es posible, simplificando los vectores directores, tenemos que:
$s\equiv\begin{cases} y-5$

También lo podemos obtener a partir del producto vectorial de los vectores normales a los planos que determinan la recta $s$

$s\equiv\begin{cases} y-5$

$\vec{u}_{s}\equiv\vec{n}_{1}\times\vec{n}_{2}=\left(\left|\begin{array}{cc} 1$

Vector director de la recta $r$

$\vec{u}_{r}=\vec{u}_{s}\times\vec{n}_{\pi}=\left(\left|\begin{array}{cc} 0$

Punto $P$ intersección de ambas rectas. Podemos obtenerlo de varias formas, dos de ellas son:

Si hemos optado por hallar las ecuaciones paramétricas de $s$ podemos hallar el punto $P$ a partir de ellas y de la ecuación del plano $\pi_{o}\equiv33x-9y-12z=0$ :
$\left(33\right)\cdot\left(8u-4\right)+\left(-9\right)\cdot\left(5\right)+\left(-12\right)\cdot\left(5-6u\right)=0$ $\Rightarrow336u-237=0\Rightarrow u=\frac{79}{112}$
el punto $P$ de intersección se obtiene sustituyendo el valor anterior del parámetro en la ecuación de la recta $s$ .
$P\left\{ \begin{array}{ccc} x$

Resolvemos el sistema para hallar el punto de intersección de la recta $s$ y el plano $\pi_{o}$
$\begin{cases} y-5$
El sistema, en forma matricial $A\cdot X=B$ , se puede escribir como:
$\left(\begin{matrix}0$
Calculemos el determinante de $A$

$\left|A\right|=\begin{vmatrix}0$ $\begin{array}{c} \begin{vmatrix}0$
$=\left[0\cdot0\left(-12\right)+3\left(-9\right)0+33\cdot1\cdot4\right]-\left[0\cdot0\cdot33+4\left(-9\right)0+\left(-12\right)1\cdot3\right]$ $=\left(132\right)-\left(-36\right)=168$
Como $\left|A\right|\mathrel{\char`≠}0\Rightarrow Rango(A)=Rango(A^{*})=3$ tenemos un SCD (tiene una sola solución). Si hallamos la solución por Cramer:

$\left|A_{x}\right|=\begin{vmatrix}5$ $\begin{array}{c} \begin{vmatrix}5$
$=\left[5\cdot0\left(-12\right)+8\left(-9\right)0+0\cdot1\cdot4\right]-\left[0\cdot0\cdot0+4\left(-9\right)5+\left(-12\right)1\cdot8\right]$ $=\left(0\right)-\left(-276\right)=276$
$\Rightarrow x=\dfrac{\begin{vmatrix}5$

$\left|A_{y}\right|=\begin{vmatrix}0$ $\begin{array}{c} \begin{vmatrix}0$
$=\left[0\cdot8\left(-12\right)+3\cdot0\cdot0+33\cdot5\cdot4\right]-\left[0\cdot8\cdot33+4\cdot0\cdot0+\left(-12\right)5\cdot3\right]$ $=\left(660\right)-\left(-180\right)=840$
$\Rightarrow y=\dfrac{\begin{vmatrix}0$

$\left|A_{z}\right|=\begin{vmatrix}0$ $\begin{array}{c} \begin{vmatrix}0$
$=\left[0\cdot0\cdot0+3\left(-9\right)5+33\cdot1\cdot8\right]-\left[5\cdot0\cdot33+8\left(-9\right)0+0\cdot1\cdot3\right]$ $=\left(129\right)-\left(0\right)=129$
$\Rightarrow z=\dfrac{\begin{vmatrix}0$

En cualquier caso:

$P$ $\left\{ \begin{aligned}x$

Finalmente, a partir del punto $P\left(\frac{23}{14},\ 5,\ \frac{43}{56}\right)$ y el vector director $\vec{u}_{r}\left(-9,\ -17,\ -12\right)$ tenemos la ecuación paramétrica de la recta $r$ es
$r\equiv\left\{ \begin{array}{cc} x=$

Enlaces al fichero fuente y al pdf final de una posible compilación.

[1]	En todos los casos, si se puede se simplifican los vectores directores/normales dividiendo por el $mcd$ de sus coordenadas.